The slope-intercept form is frequently used in algebra to measure the equation of the straight- line. The straight-line equation also known as the LINEAR EQUATION is widely used in algebraic expressions. It can be found by using various algebraic methods.
The slope-intercept form, point-slope form, two points form and intercept form are the well-known algebraic methods to measure the straight line’s equation. In this article, we’ll learn about the slope-intercept form with a lot of examples.

What is a slope-intercept form?

In algebra, the slope-intercept form is one of the various methods used to measure the
equation of the straight line. The other methods are two points form, point-slope form, and intercept form.

The Slope-intercept form uses an equation to express the equation of the straight line.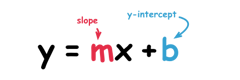
• In the equation of the slope-intercept form, x & y are the fixed points of the line.
• m is the line’s slope.
• b is the y-intercept.

To calculate the slope-intercept form, you have to calculate the slope of the line and the y intercept form of the equation. The measure of the steepness of the line is known as a slope. The slope is widely used in algebra. You can calculate the slope by using the general equation of the slope. The slope can be calculated by using a fraction of the change in the points of y (rise) over the change in the points of x (run).

The equation of the slope is given below-

                 Slope of the line = m = rise / run
                 Slope of the line = m = 𝚫y/ 𝚫x
                 Slope of the line = m = y2 – y1/ x2– x1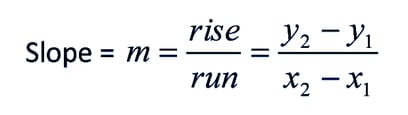If the slope is not given in the equation of the slope-intercept form, you have to calculate it first by using the points of the line. After calculating the slope of the line put a pair of numbers and calculated slope in the equation of the slope-intercept form to calculate the y-intercept.

How to calculate the straight line’s equation by using a slope-intercept form?

The equation of the straight line can be calculated easily by using the equation of the slope intercept form. Follow the below steps to measure the linear equation of the line.

• Identify the given points of the line.
• Find the slope of the line by using the given points.
• Use the calculated slope and a pair of numbers to calculate the y-intercept of the line.
• Substitute the terms of slope and y-intercept in the general formula of the slope intercept form.
• The result will be the linear equation of the line.
  
  You can also use a slope intercept form calculator to get the step by step solution in a couple of seconds. Follow the below steps to calculate the linear equation of the line using this tool.

Step 1: First of all, select the input option i.e., two points, one point, and slope, or y-intercept and the slope.
                       I Have :
Step 2 : Input the given value.

                    I Have :

Step 3 : Hit the calculate button to get the result.

Step 4: The result with the steps will show below the calculate button.

                                      RESULT

                                       Slope Intercept Form
Let us take some examples to learn how to calculate the equation of the line.

• Example 1: For positive integers
  Find the equation of the straight line of (13, 21) and (10, 23) by using a slope-intercept form.
  Solution-
  Step 1: First of all, identify the given points.

              x1 = 21, x2 = 23, y1 = 13, y2 = 10

    Step 2: Find the slope of the line by using the given points.

Slope of the line,

                   m = 𝚫y/ 𝚫x

                   m = y2 – y1/ x2 – x1
                   m = (10 – (13)) / (23 – 21)
                   m = (10 – 13) / (23 – 21)
                   m = (– 3) / (2)
                   m = – 3 / 2
                   m = -1.5

     Step 3: Write the general formula of the slop-intercept form.

                                                  y = mx + b

     Step 4: Put the calculated slope in the formula of the slope intercept form.

                                                  y = mx + b

                                                 y = -1.5x + 40.5

• Example 2: For negative integers
  Find the equation of the straight line of (-3, -1) and (-20, -21) by using a slope-intercept form.
  Solution
   Step 1: First of all, identify the given points.

                   x1 = -3, x2 = -20, y1 = -1, y2 = -21

     Step 2: Find the slope of the line by using the given points.
Slope of the line,

                       m = 𝚫y/ 𝚫x
                       m = y2 – y1/ x2 – x1
                       m = (-21 – (-1)) / (-20 – (-3))
                       m = (-21 + 1) / (-20 + 3)
                       m = (-20) / (-17)
                       m = 20 / 17
                       m = 1.1765

    Step 3: Write the general formula of the slop-intercept form.
                                    y = mx + b

     Step 4: Put the calculated slope in the formula of slope intercept form.

                                       y = mx + b
                                       y = 1.1765x + b
     Step 5: Find the y intercept of the slope-intercept form by putting any pair of points and slope of lines.
                                      y = 1.1765x + b
                                     -1 = 1.1765(-3) + b
                                      -1 = -3.5295 + b
                                      -1 + 3.5295 = b
                                        2.5295 = b
                                y-intercept = b = 2.5295

     Step 6: Substitute the calculated values in the formula of the slope-intercept form.
                                    y = mx + b
                                    y = 1.1765x + 2.5295

Summary
In algebra, the slope-intercept form is the most frequently used method to express the linear equation of the line. in this article, we have discussed all the basics of this method. Now you can solve any problem easily related to the slope.

A note from the author:

I'm a mathematician. I'm writing the articles for the kids and grade 11 & 12 students. I write mostly on the various topics of calculus & algebra like derivative, integral, slope, slope intercept form, limits, etc.
I am a sophomore psych major at Case Western Reserve University. In the future, I plan on researching influence to help people improve their lives. I'm a senior psychology student with a minor in marketing at Case Western Reserve University. In the past, I've interned for a number of nonprofits and for-profit organizations, including a collaboration between Paragon One and Meta, formerly known as Facebook. I like walking around outdoors, exploring new places, and creating personalized greeting cards. I am a 3rd year college student studying cognitive science and minoring in marketing. I love learning about how the human brain works, and applying my knowledge of cognitive science and marketing to help improve the lives of others.